The Kozeny Carman Equation
The Kozeny–Carman equation is used in the field of fluid dynamics to calculate the pressure drop of a fluid flowing through a packed bed of solid particles. This equation relates the permeability of tube packed with particles to interparticle porosity, bed morphology and particle size and shape. The model replaces the space between the particles as a set of capillaries and accounts for the difference in length of the hypothetical capillaries (equation 2.8).
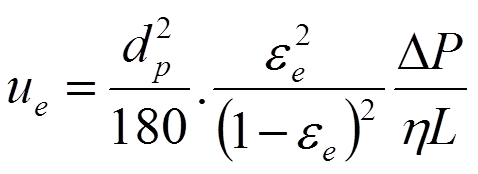
It is imperative to be aware that the original K-C equation is based on interstitial velocity. Combining equation 2.8 with equation 2.3 leads to:
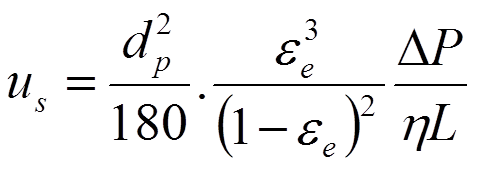
The constants in this equation are combined in a dimensionless factor called the "column resistance factor".
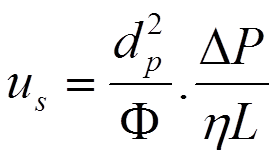
In practical work one may assume an interparticle porosity of 0.4 which delivers after substitution a value of 1012.5 for the column resistance factor. Smaller values of εe result in higher values of the column resistance factor and mean a less permeable column. Higher values of εe result in smaller values of the column resistance factor and therefore more permeable column. The minimum value of the column resistance factor is 32 which applies to an empty tube.
One needs to be aware that this is a very global treatment. For more detailed treatment one is referred to recent work by the Desmet group from the Free University of Brussels and by the Tallarek group at the Phillips University of Marburg in Germany.
